On va aborder dans ce sujet le dimensionnement des tirants de suspension, vis-à-vis des principaux efforts vus par ces tirants en fonctionnement : Efforts de traction, de freinage et les chocs.
Le cas sera développé pour le pont arrière, mais tout peut bien sur le transposer pour un pont avant.
Partie 1 : Détermination des efforts en fonctionnement
Cas 1 : Traction ou Freinage
Le cas sera développé pour la traction, mais le cas de freinage s’obtient facilement en inversant le sens des sollicitations.
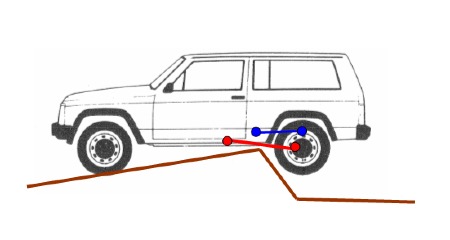
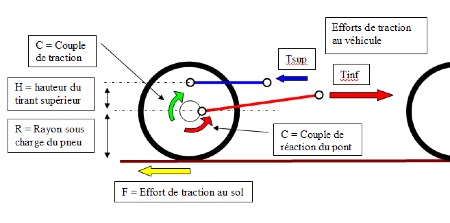
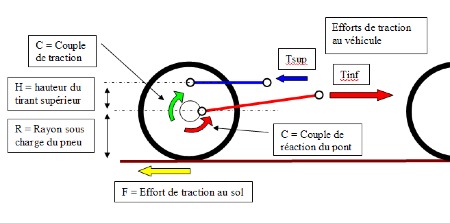
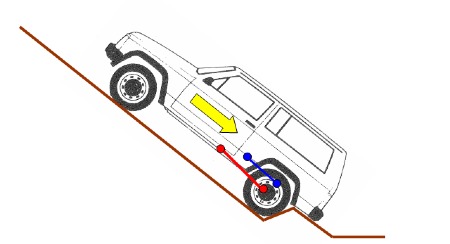
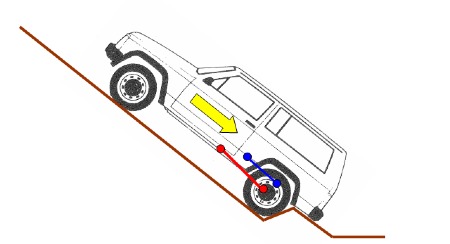
L’effort de traction ou de freinage passe par le point de contact du pneu au sol :
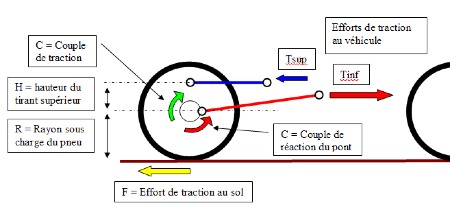
Le tirant inférieur ne peut pas reprendre les efforts liés au couple de traction car son articulation coté pont est généralement au niveau de l’axe du moyeu.
Les tirants supérieurs servent à reprendre le couple, l’effort horizontal de traction se réparti donc entre les tirants inférieurs et supérieurs par la relation suivante :
Tirant supérieur (tendu) : Tsup=C/H comme le couple de traction c’est C=F*R, on a Tsup=F*R/H
Tirant inférieur (comprimé) : Tinf = F + F*R/H = F(1+R/H)
L’effort maximal que l’on peut transmettre au sol est limité par le coefficient d’adhérence du pneu sur le sol, sur un sol sec très adhérent, ce coefficient est proche de 1.
L’effort au sol ne peut donc pas dépasser la charge verticale au pneu, au delà ça patine !
Donc si le véhicule a un différentiel libre, l’effort maxi à la roue ne dépasse pas 50% du poids de l’essieu, mais on peut atteindre 100% avec un blocage et dans certaines circonstances (gros croisement, avec tout le poids arrière sur une roue).
Comme on est sur Pirate4x4.fr, on va partir sur cette hypothèse très sévère…
Exemple :
Véhicule d’environ 1500 Kg, dont 700 Kg sur l’essieu arrière, donc effort horizontal maxi F= 7000 N
Pneus en 31, donc rayon sous charge R=0.4 m
H = 0.2 m
Le couple maximal de traction est donc C = F*R = 7000*0.4 = 2800 N.m
On trouve donc Tsup = C/H = 2800/0.2 = 14000 N (1.4 Tonnes)
Tinf = F+F*R/H = 7000 + 7000*0.4/0.2 = 7000+14000 = 21000 N (2.1 Tonne)
On poursuit maintenant avec le tirant inférieur, qui est le plus sollicité, mais le même raisonnement peut s’appliquer sur le tirant supérieur.
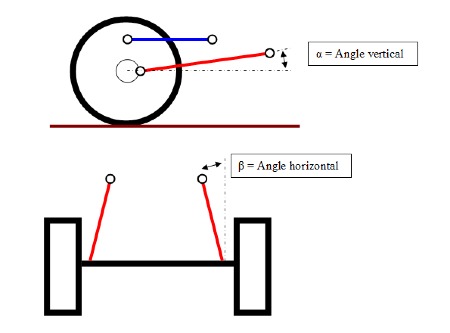
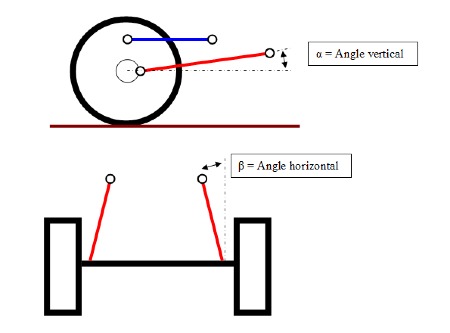
Maintenant que l’on a estimé l’effort horizontal maximal, on va en déduire l’effort dans le tirant, pour cela il faut déterminer les angles dans le plan horizontal et vertical que forme le tirant.
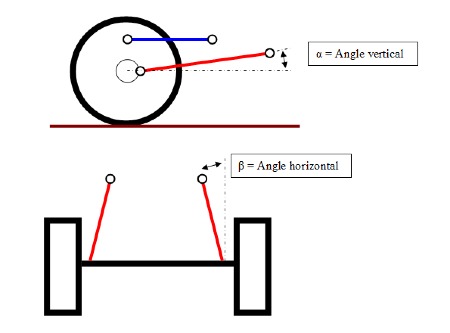
L’effort dans l’axe du tirant est déterminé par la relation : Tinf/(Cos(a)*Cos(b))
Toujours pour notre exemple :
Alpha = 20°
Beta = 5°
Effort dans le tirant = Tinf/(cos20°*cos5°) = 21000/(0.94*0.99) = 22433 N (2.24 Tonnes)
Remarque : plus les tirants sont inclinés et plus ils sont sollicités pour le même effort horizontal.
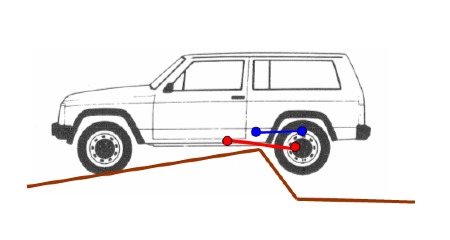
Cas 2 : Choc sur un obstacle
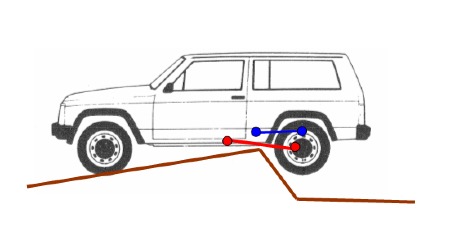
C’est à mon avis le cas le plus dimensionnant et pour lequel on a souvent vu des ruptures ou des déformation excessives des tirants de ponts, souvent par flambage.
Le risque vient après un échec de franchissement où le véhicule recule dans la pente, et une roue arrière stop brutalement le véhicule sur un obstacle.
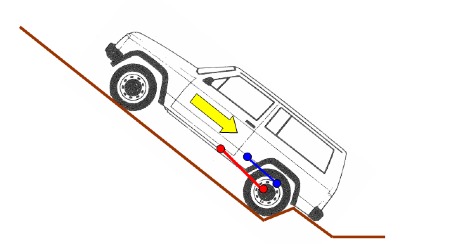
Exemple ici avec un Disco qui « flambe » son tirant arrière :

Le pont tourne, le croisillon se bloque, et quand le véhicule repart, l’arbre de transmission se découpe.
L’estimation des efforts en jeux est plus difficile car cela dépend de la décélération, donc de la vitesse avant le choc, de la masse du véhicule et de la raideur du pneu.
On peut cependant fixer une valeur de la décélération, à au moins 3G, valeur couramment utilisée pour dimensionner les trains roulants des véhicules de route (les plates quoi )
)
Donc pour notre véhicule de 1500 Kg, cela donne F=M*gamma=1500*3*10=45000 N = 4.5 Tonnes.
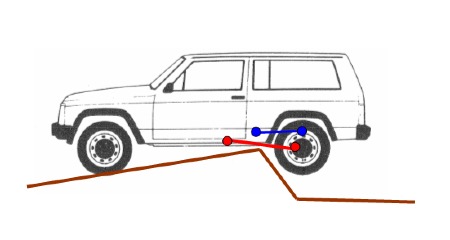
Cas 3 : Appui sur le tirant
C’est le cas le plus simple pour déterminer les efforts, on se basera sur le poids à l’essieu arrière :
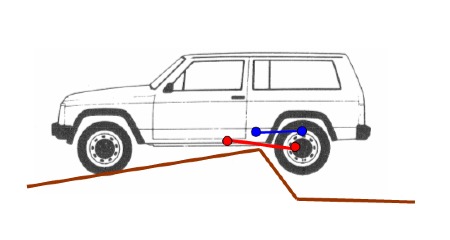
Sur un véhicule de série les tirants ne sont pas trop longs, ce qui limite le risque d’appui au milieu du tirant, qui est le cas le plus sévère pour la résistance en flexion.
Partie 2 : Dimensionnement des tirants
Maintenant que l’on a une idée des efforts en jeux, on peut s’occuper du dimensionnement.
Tirant en traction
Ce cas ne pose pas trop de problème, la contrainte de traction dans le tirant est facilement obtenu en divisant l’effort axial par la section du tirant.
Effort admissible pour les principaux tubes en se basant sur une limite élastique :
Tube de chauffage (limite élastique à 235 MPa)
Tube 48.3 mm : 10 tonnes
Tube 42.4 mm : 8.7 tonnes
Tube 33.7 mm : 6.8 tonnes
TubeT3 (limite élastique 355 MPa)
Tube 48.3 mm : 15.2 tonnes
Tube 42.4 mm : 13.2 tonnes
Tube 33.7 mm : 10.3 tonnes
Tirant en compression
La contrainte de compression dans le tirant se détermine exactement comme pour la sollicitation en traction.
La particularité du cas en compression c’est le risque de flambement.
Le flambement est une instabilité qui fait fléchir le tirant et qui intervient brutalement sans quasiment prévenir.
On peut facilement appréhender le problème avec un simple réglet métallique que l’on appui verticalement sur une table.
La charge critique théorique est déterminée par la formule d’Euler :
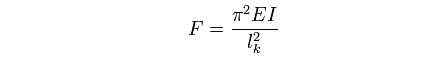
Avec :
E : Module d’élasticité du matériau
I : Inertie quadratique de la section
L : Longueur axe à axe du tirant
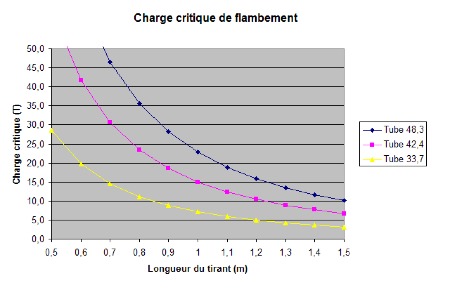
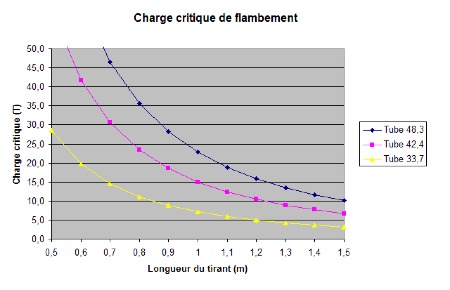
On remarque que cette charge critique diminue fortement avec l’augmentation de la longueur du tirant à section constante.
Autre point intéressant, la charge critique ne dépend absolument pas de la limite élastique du matériau, autrement dit un tirant en tube de chauffage aura la même charge critique que le même en acier Chrome Molybdène
Pour augmenter la charge critique il faut donc augmenter le diamètre du tirant.
Comparatif des charges critiques pour les principales tailles de tubes :
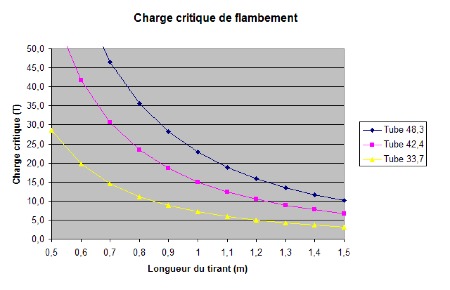
Comparatif tube / barre pleine
Si on veut la même charge critique que les tubes voici les diamètres des barres pleines :
Tube 33.7 mm => Barre pleine diamètre 29 mm
Tube 42.4 mm => Barre pleine diamètre 35 mm
Tube 48.3 mm => Barre pleine diamètre 38.5 mm
Je vous laisse calculer la différence de poids, mais clairement la barre pleine n’est pas l’optimum.
Cas particulier du tirant coudé
La charge critique de flambement est un peu plus complexe à calculer :
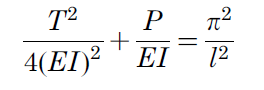
L’excentration du tirant ne réduit que faiblement la capacité au flambement, par contre elle impacte directement sa résistance à la flexion.
La contrainte de flexion au maximum de l’excentration est :
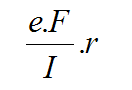
Avec :
e : Excentration
I : Inertie quadratique
r : rayon maxi du tube
F : Effort dans l’axe du tirant
Si on prend l’exemple du tirant coudé de capitaine :

Avec une excentration estimée à 75mm sur la photo (à confirmer par The Bargeots) voici le comparatif tirant droit d’origine, tirant coudé d’origine, triant renforcé :
Tirant d’origine Patrol
Dext = 32mm
Epaisseur = 2.5 mm
Longueur = 645 mm
Charge de compression max = 5.4 Tonnes
Tirant Patrol coudé à la "Red Neck"
Dext = 32mm
Epaisseur = 2.5 mm
Longueur = 645 mm
Excentration = 75 mm
Charge de compression max = 450 Kg
C'est minable et cela montre bien l'impact de l'excentration
Tirant coudé et manchonné (épaisseur 6mm en 20Mv6)
Dext = 32mm
Epaisseur = 2.5 mm + 6 mm
Longueur = 645 mm
Excentration = 75 mm
Charge de compression max = 3.9 Tonnes
Mise à jour du 23/08/2011 :
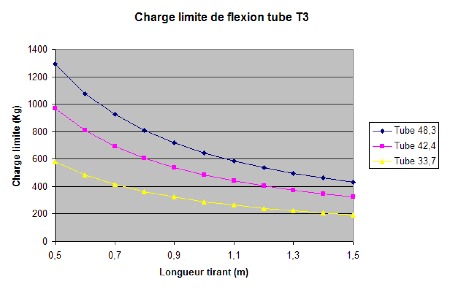
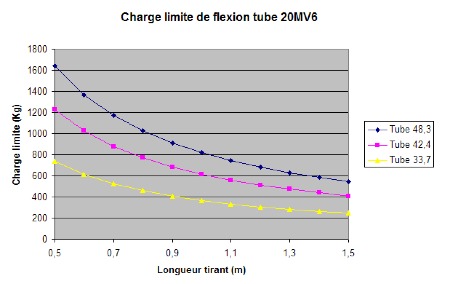
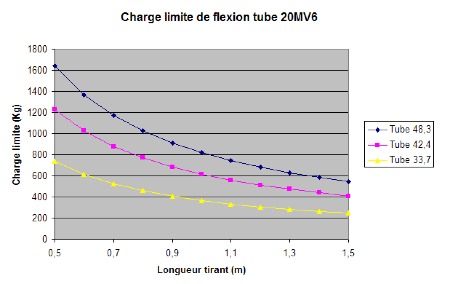
Tirant en flexion
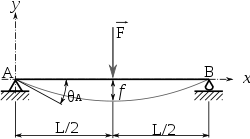
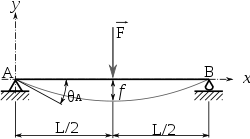
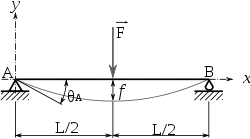
Pour le tirant en flexion, le cas le plus sollicitant c’est quand l’appui se produit au milieu du tirant :
Le moment de flexion maximum est : M=FL/4
La contrainte de flexion est M.R/I
Avec :
M le moment de flexion
R le rayon externe du tube
I l’inertie quadratique du tube :

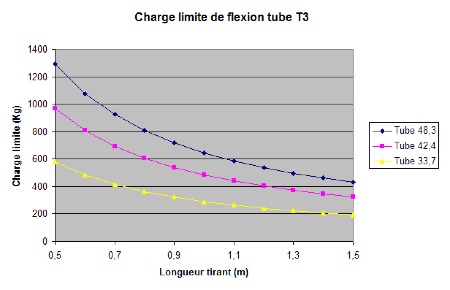
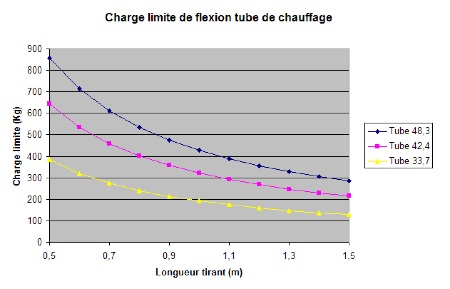
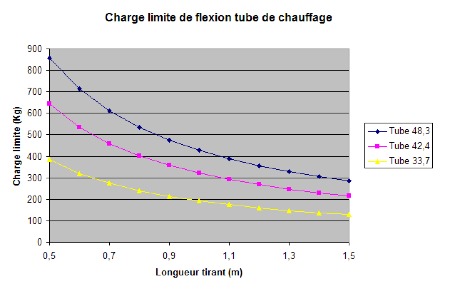
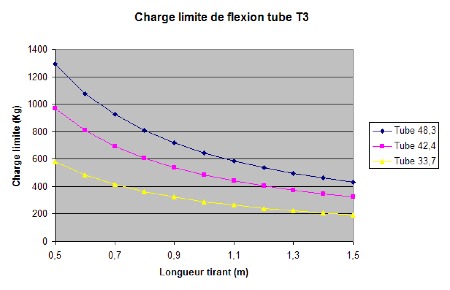
Comparatif des charges critiques pour les principales tailles de tubes :
Tube de chauffage (235 MPa) :

Tube T3 (355 MPa) :
Tube 20Mv6 (450 MPa) :
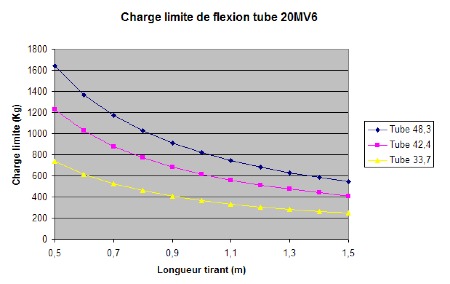
Donc si on n’a pas du tube à haute résistance, il faut utiliser des tubes de fort diamètre.
[FONT="]
[/FONT]
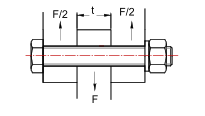
Résistance des boulons au cisaillement
Deux montages sont possibles :
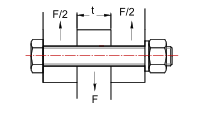
Simple cisaillement : La rotule n’est tenue que par un coté, c’est le montage utilisé pour des efforts modéré :

Double cisaillement : La rotule est montée dans une chape, les efforts de cisaillement sont répartis sur deux sections de la vis, c’est le montage le plus courant avec des embouts à rotules.
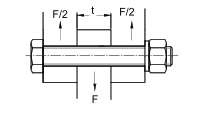
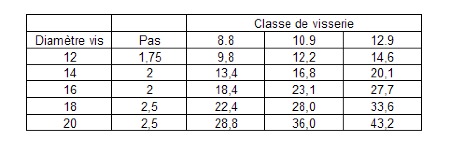
Charge admissible au double cisaillement (tonnes) :
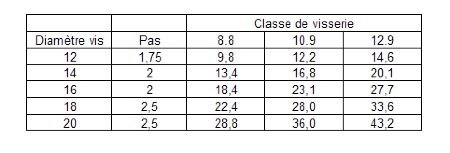
Il n’est pas conseillé d’utiliser de la visserie de classe 12.9 (ou au dessus) car si ces vis ont une plus forte limite élastique ou de rupture, elles ont cependant un potentiel plus faible en énergie de déformation, hors dans une sollicitation rapide au choc, c’est plus la ténacité qui compte que l’effort maximum admissible.
Julien.
Le cas sera développé pour le pont arrière, mais tout peut bien sur le transposer pour un pont avant.
Partie 1 : Détermination des efforts en fonctionnement
Cas 1 : Traction ou Freinage
Le cas sera développé pour la traction, mais le cas de freinage s’obtient facilement en inversant le sens des sollicitations.
L’effort de traction ou de freinage passe par le point de contact du pneu au sol :

Le tirant inférieur ne peut pas reprendre les efforts liés au couple de traction car son articulation coté pont est généralement au niveau de l’axe du moyeu.
Les tirants supérieurs servent à reprendre le couple, l’effort horizontal de traction se réparti donc entre les tirants inférieurs et supérieurs par la relation suivante :
Tirant supérieur (tendu) : Tsup=C/H comme le couple de traction c’est C=F*R, on a Tsup=F*R/H
Tirant inférieur (comprimé) : Tinf = F + F*R/H = F(1+R/H)
L’effort maximal que l’on peut transmettre au sol est limité par le coefficient d’adhérence du pneu sur le sol, sur un sol sec très adhérent, ce coefficient est proche de 1.
L’effort au sol ne peut donc pas dépasser la charge verticale au pneu, au delà ça patine !
Donc si le véhicule a un différentiel libre, l’effort maxi à la roue ne dépasse pas 50% du poids de l’essieu, mais on peut atteindre 100% avec un blocage et dans certaines circonstances (gros croisement, avec tout le poids arrière sur une roue).
Comme on est sur Pirate4x4.fr, on va partir sur cette hypothèse très sévère…
Exemple :
Véhicule d’environ 1500 Kg, dont 700 Kg sur l’essieu arrière, donc effort horizontal maxi F= 7000 N
Pneus en 31, donc rayon sous charge R=0.4 m
H = 0.2 m
Le couple maximal de traction est donc C = F*R = 7000*0.4 = 2800 N.m
On trouve donc Tsup = C/H = 2800/0.2 = 14000 N (1.4 Tonnes)
Tinf = F+F*R/H = 7000 + 7000*0.4/0.2 = 7000+14000 = 21000 N (2.1 Tonne)
On poursuit maintenant avec le tirant inférieur, qui est le plus sollicité, mais le même raisonnement peut s’appliquer sur le tirant supérieur.
Maintenant que l’on a estimé l’effort horizontal maximal, on va en déduire l’effort dans le tirant, pour cela il faut déterminer les angles dans le plan horizontal et vertical que forme le tirant.

L’effort dans l’axe du tirant est déterminé par la relation : Tinf/(Cos(a)*Cos(b))
Toujours pour notre exemple :
Alpha = 20°
Beta = 5°
Effort dans le tirant = Tinf/(cos20°*cos5°) = 21000/(0.94*0.99) = 22433 N (2.24 Tonnes)
Remarque : plus les tirants sont inclinés et plus ils sont sollicités pour le même effort horizontal.
Cas 2 : Choc sur un obstacle
C’est à mon avis le cas le plus dimensionnant et pour lequel on a souvent vu des ruptures ou des déformation excessives des tirants de ponts, souvent par flambage.
Le risque vient après un échec de franchissement où le véhicule recule dans la pente, et une roue arrière stop brutalement le véhicule sur un obstacle.

Exemple ici avec un Disco qui « flambe » son tirant arrière :

Le pont tourne, le croisillon se bloque, et quand le véhicule repart, l’arbre de transmission se découpe.
L’estimation des efforts en jeux est plus difficile car cela dépend de la décélération, donc de la vitesse avant le choc, de la masse du véhicule et de la raideur du pneu.
On peut cependant fixer une valeur de la décélération, à au moins 3G, valeur couramment utilisée pour dimensionner les trains roulants des véhicules de route (les plates quoi
Donc pour notre véhicule de 1500 Kg, cela donne F=M*gamma=1500*3*10=45000 N = 4.5 Tonnes.
Cas 3 : Appui sur le tirant
C’est le cas le plus simple pour déterminer les efforts, on se basera sur le poids à l’essieu arrière :

Sur un véhicule de série les tirants ne sont pas trop longs, ce qui limite le risque d’appui au milieu du tirant, qui est le cas le plus sévère pour la résistance en flexion.
Partie 2 : Dimensionnement des tirants
Maintenant que l’on a une idée des efforts en jeux, on peut s’occuper du dimensionnement.
Tirant en traction
Ce cas ne pose pas trop de problème, la contrainte de traction dans le tirant est facilement obtenu en divisant l’effort axial par la section du tirant.
Effort admissible pour les principaux tubes en se basant sur une limite élastique :
Tube de chauffage (limite élastique à 235 MPa)
Tube 48.3 mm : 10 tonnes
Tube 42.4 mm : 8.7 tonnes
Tube 33.7 mm : 6.8 tonnes
TubeT3 (limite élastique 355 MPa)
Tube 48.3 mm : 15.2 tonnes
Tube 42.4 mm : 13.2 tonnes
Tube 33.7 mm : 10.3 tonnes
Tirant en compression
La contrainte de compression dans le tirant se détermine exactement comme pour la sollicitation en traction.
La particularité du cas en compression c’est le risque de flambement.
Le flambement est une instabilité qui fait fléchir le tirant et qui intervient brutalement sans quasiment prévenir.
On peut facilement appréhender le problème avec un simple réglet métallique que l’on appui verticalement sur une table.
La charge critique théorique est déterminée par la formule d’Euler :
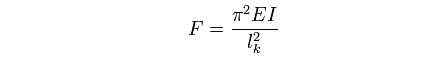
Avec :
E : Module d’élasticité du matériau
I : Inertie quadratique de la section
L : Longueur axe à axe du tirant
On remarque que cette charge critique diminue fortement avec l’augmentation de la longueur du tirant à section constante.
Autre point intéressant, la charge critique ne dépend absolument pas de la limite élastique du matériau, autrement dit un tirant en tube de chauffage aura la même charge critique que le même en acier Chrome Molybdène

Pour augmenter la charge critique il faut donc augmenter le diamètre du tirant.
Comparatif des charges critiques pour les principales tailles de tubes :

Comparatif tube / barre pleine
Si on veut la même charge critique que les tubes voici les diamètres des barres pleines :
Tube 33.7 mm => Barre pleine diamètre 29 mm
Tube 42.4 mm => Barre pleine diamètre 35 mm
Tube 48.3 mm => Barre pleine diamètre 38.5 mm
Je vous laisse calculer la différence de poids, mais clairement la barre pleine n’est pas l’optimum.
Cas particulier du tirant coudé
La charge critique de flambement est un peu plus complexe à calculer :
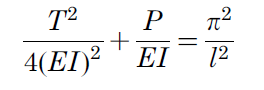
L’excentration du tirant ne réduit que faiblement la capacité au flambement, par contre elle impacte directement sa résistance à la flexion.
La contrainte de flexion au maximum de l’excentration est :
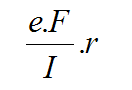
Avec :
e : Excentration
I : Inertie quadratique
r : rayon maxi du tube
F : Effort dans l’axe du tirant
Si on prend l’exemple du tirant coudé de capitaine :

Avec une excentration estimée à 75mm sur la photo (à confirmer par The Bargeots) voici le comparatif tirant droit d’origine, tirant coudé d’origine, triant renforcé :
Tirant d’origine Patrol
Dext = 32mm
Epaisseur = 2.5 mm
Longueur = 645 mm
Charge de compression max = 5.4 Tonnes
Tirant Patrol coudé à la "Red Neck"
Dext = 32mm
Epaisseur = 2.5 mm
Longueur = 645 mm
Excentration = 75 mm
Charge de compression max = 450 Kg
C'est minable et cela montre bien l'impact de l'excentration
Tirant coudé et manchonné (épaisseur 6mm en 20Mv6)
Dext = 32mm
Epaisseur = 2.5 mm + 6 mm
Longueur = 645 mm
Excentration = 75 mm
Charge de compression max = 3.9 Tonnes
Mise à jour du 23/08/2011 :
Tirant en flexion
Pour le tirant en flexion, le cas le plus sollicitant c’est quand l’appui se produit au milieu du tirant :

Le moment de flexion maximum est : M=FL/4

La contrainte de flexion est M.R/I
Avec :
M le moment de flexion
R le rayon externe du tube
I l’inertie quadratique du tube :

Comparatif des charges critiques pour les principales tailles de tubes :
Tube de chauffage (235 MPa) :

Tube T3 (355 MPa) :

Tube 20Mv6 (450 MPa) :

Donc si on n’a pas du tube à haute résistance, il faut utiliser des tubes de fort diamètre.
[FONT="]
[/FONT]
Résistance des boulons au cisaillement
Deux montages sont possibles :
Simple cisaillement : La rotule n’est tenue que par un coté, c’est le montage utilisé pour des efforts modéré :

Double cisaillement : La rotule est montée dans une chape, les efforts de cisaillement sont répartis sur deux sections de la vis, c’est le montage le plus courant avec des embouts à rotules.

Charge admissible au double cisaillement (tonnes) :

Il n’est pas conseillé d’utiliser de la visserie de classe 12.9 (ou au dessus) car si ces vis ont une plus forte limite élastique ou de rupture, elles ont cependant un potentiel plus faible en énergie de déformation, hors dans une sollicitation rapide au choc, c’est plus la ténacité qui compte que l’effort maximum admissible.
Julien.
Fichiers joints
-
 schema10.png14.3 KB · Affichages: 4
schema10.png14.3 KB · Affichages: 4 -
 schema11.png9 KB · Affichages: 4
schema11.png9 KB · Affichages: 4 -
 schema10.png14.3 KB · Affichages: 2
schema10.png14.3 KB · Affichages: 2 -
 schema12.png39.8 KB · Affichages: 2
schema12.png39.8 KB · Affichages: 2 -
 schema11.png9 KB · Affichages: 2
schema11.png9 KB · Affichages: 2 -
 p5200810.jpg53.3 KB · Affichages: 2
p5200810.jpg53.3 KB · Affichages: 2 -
 schema12.png39.8 KB · Affichages: 2
schema12.png39.8 KB · Affichages: 2 -
 schema13.png34 KB · Affichages: 2
schema13.png34 KB · Affichages: 2 -
 p5200810.jpg53.3 KB · Affichages: 2
p5200810.jpg53.3 KB · Affichages: 2 -
 schema13.png34 KB · Affichages: 2
schema13.png34 KB · Affichages: 2 -
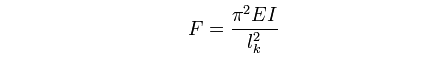 equati10.png1 KB · Affichages: 1
equati10.png1 KB · Affichages: 1 -
 equati10.png1 KB · Affichages: 1
equati10.png1 KB · Affichages: 1 -
 graph_10.png7.9 KB · Affichages: 0
graph_10.png7.9 KB · Affichages: 0 -
 graph_10.png7.9 KB · Affichages: 0
graph_10.png7.9 KB · Affichages: 0 -
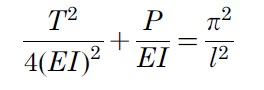 equati13.png3.3 KB · Affichages: 0
equati13.png3.3 KB · Affichages: 0 -
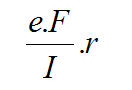 equati12.png666 bytes · Affichages: 0
equati12.png666 bytes · Affichages: 0 -
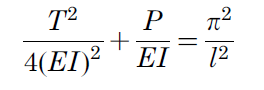 equati13.png3.3 KB · Affichages: 0
equati13.png3.3 KB · Affichages: 0 -
 tirant10.png179.1 KB · Affichages: 0
tirant10.png179.1 KB · Affichages: 0 -
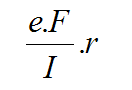 equati12.png666 bytes · Affichages: 0
equati12.png666 bytes · Affichages: 0 -
 schema13.png34 KB · Affichages: 0
schema13.png34 KB · Affichages: 0 -
 tirant10.png179.1 KB · Affichages: 0
tirant10.png179.1 KB · Affichages: 0 -
 250px-Poutre_appuis_trois_points.svg.png6.2 KB · Affichages: 0
250px-Poutre_appuis_trois_points.svg.png6.2 KB · Affichages: 0 -
 schema13.png34 KB · Affichages: 0
schema13.png34 KB · Affichages: 0 -
 250px-Poutre_appuis_trois_points.svg.png6.2 KB · Affichages: 0
250px-Poutre_appuis_trois_points.svg.png6.2 KB · Affichages: 0 -
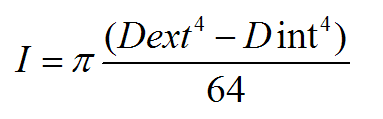 equati14.png2 KB · Affichages: 0
equati14.png2 KB · Affichages: 0 -
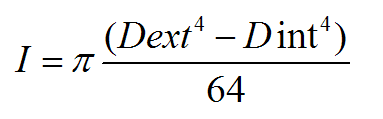 equati14.png2 KB · Affichages: 0
equati14.png2 KB · Affichages: 0 -
 graph_11.png7.3 KB · Affichages: 0
graph_11.png7.3 KB · Affichages: 0 -
 graph_11.png7.3 KB · Affichages: 0
graph_11.png7.3 KB · Affichages: 0 -
 graph_12.png6.9 KB · Affichages: 0
graph_12.png6.9 KB · Affichages: 0 -
 graph_12.png6.9 KB · Affichages: 0
graph_12.png6.9 KB · Affichages: 0 -
 graph_13.png7.3 KB · Affichages: 0
graph_13.png7.3 KB · Affichages: 0 -
 534v310.jpg15.3 KB · Affichages: 0
534v310.jpg15.3 KB · Affichages: 0 -
 cisail10.png2.1 KB · Affichages: 0
cisail10.png2.1 KB · Affichages: 0 -
 graph_13.png7.3 KB · Affichages: 0
graph_13.png7.3 KB · Affichages: 0 -
 534v310.jpg15.3 KB · Affichages: 1
534v310.jpg15.3 KB · Affichages: 1 -
 tablea10.png4.2 KB · Affichages: 2
tablea10.png4.2 KB · Affichages: 2 -
 cisail10.png2.1 KB · Affichages: 2
cisail10.png2.1 KB · Affichages: 2 -
 tablea10.png4.2 KB · Affichages: 2
tablea10.png4.2 KB · Affichages: 2
Dernière édition:




